Probability#
Probability theory talks about the construction and implications of probability models. For example, given a probability distribution, what are the mean and variance? What is the distribution of a transformed random variable? In computer simulations, probability theory tells us what will happen to the generated realizations, in particular when the experiments can be repeated as many times as the researcher wishes. This is a real-world analogue of the frequentist’s interpretation of probability.
Probability Space#
A sample space \(\Omega\) is a collection of all possible outcomes. It is a set of things.
An event \(A\) is a subset of \(\Omega\). It is something of interest on the sample space.
A \(\sigma\)-field is a complete set of events that include all countable unions, intersections, and differences. It is a well-organized structure built on the sample space.
A probability measure satisfies
(positiveness) \(P\left(A\right)\geq0\) for all events;
(countable additivity) If \(A_{i}\), \(i\in\mathbb{N}\), are mutually disjoint, then \(P\left(\bigcup_{i\in\mathbb{N}}A_{i}\right)=\sum_{i\in\mathbb{N}} P \left(A_{i}\right).\)
\(P(\Omega) = 1\).
The above construction gives a mathematically well-defined probability measure, but we have not yet answered “How to assign the probability?”
There are two major schools of thinking on probability assignment. One is the frequentist, who considers probability as the average chance of occurrence if a large number of experiments are carried out. The other is the Bayesian, who deems probability as a subjective brief. The principles of these two schools are largely incompatible, while each school has peculiar pros and cons under different real-world contexts.
Random Variable#
A random variable maps an event to a real number. If the outcome is multivariate, we call it a random vector.
Data example
Data source: HK top 300 Youtubers. We look at the number of uploaded videos in these accounts.
import pandas as pd
# Reading the CSV file
d0 = pd.read_csv("HKTop300YouTubers.csv")
print(d0)
rank Youtuber subscribers \
0 1 Shadow MusicShadow Music 7,690,000
1 2 Emi WongEmi Wong 4,870,000
2 3 iQIYI 爱奇艺iQIYI 爱奇艺 4,010,000
3 4 South China Morning PostSouth China Morning Post 2,650,000
4 5 GEM鄧紫棋GEM鄧紫棋 2,520,000
.. ... ... ...
295 296 Jessica WongJessica Wong 69,000
296 297 昼与白鲸昼与白鲸 68,700
297 298 后宫冷婶儿后宫冷婶儿 68,600
298 299 CatGirl貓女孩CatGirl貓女孩 68,200
299 300 男人EEETV男人EEETV 66,400
video views video count category started
0 3,665,970,114 1,144 People & Blogs 2017
1 607,656,993 390 People & Blogs 2014
2 1,744,552,001 9,740 Film & Animation 2015
3 2,612,265,071 11,376 News & Politics 2007
4 1,752,111,944 77 People & Blogs 2019
.. ... ... ... ...
295 3,008,911 80 Howto & Style 2014
296 18,950,918 156 Film & Animation 2020
297 43,142,355 323 Howto & Style 2020
298 0 0 Entertainment 2015
299 7,627,706 147 Comedy 2018
[300 rows x 7 columns]
# Remove NA and zeros by replacing zeros with NaN and then dropping rows with any NaN values
d0.replace(0, pd.NA, inplace=True)
d0.dropna(inplace=True)
# Select columns 3 to 5 (Python uses 0-based indexing, adjust accordingly)
d1 = d0.iloc[:, 2:5].copy()
# Rename columns
d1.columns = ["subs", "view", "count"] # "count" is the number of videos uploaded
print( d1 )
subs view count
0 7,690,000 3,665,970,114 1,144
1 4,870,000 607,656,993 390
2 4,010,000 1,744,552,001 9,740
3 2,650,000 2,612,265,071 11,376
4 2,520,000 1,752,111,944 77
.. ... ... ...
295 69,000 3,008,911 80
296 68,700 18,950,918 156
297 68,600 43,142,355 323
298 68,200 0 0
299 66,400 7,627,706 147
[294 rows x 3 columns]
# convert string into numbers
for column in d1.columns:
d1[column] = pd.to_numeric(d1[column].str.replace(',', ''), errors='coerce')
print(d1)
subs view count
0 7690000 3665970114 1144
1 4870000 607656993 390
2 4010000 1744552001 9740
3 2650000 2612265071 11376
4 2520000 1752111944 77
.. ... ... ...
295 69000 3008911 80
296 68700 18950918 156
297 68600 43142355 323
298 68200 0 0
299 66400 7627706 147
[294 rows x 3 columns]
d1["count"]
0 1144
1 390
2 9740
3 11376
4 77
...
295 80
296 156
297 323
298 0
299 147
Name: count, Length: 294, dtype: int64
import numpy as np
# if any value is zero, remove the row
d1 = d1[(d1 != 0).all(axis=1)]
d1_log= np.log(d1)
import matplotlib.pyplot as plt
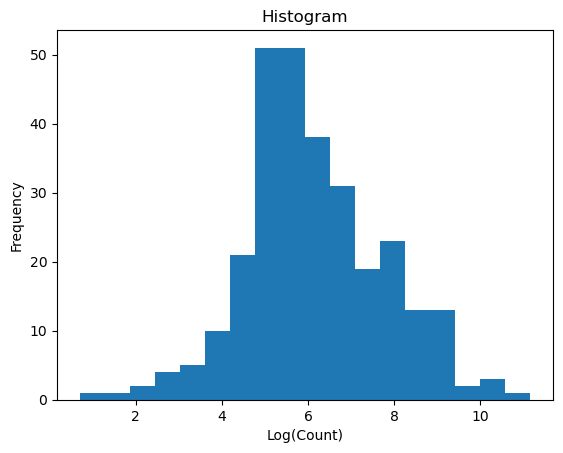
# Plotting histogram of the 'count' column after log transformation
plt.hist(d1_log['count'], bins='auto') # 'auto' lets matplotlib decide the number of bins
plt.title('Histogram')
plt.xlabel('Log(Count)')
plt.ylabel('Frequency')
plt.show()
Distribution Fun#
We go back to some terminologies we learned in an undergraduate probability course. A (cumulative) distribution function \(F:\mathbb{R}\mapsto [0,1]\) is defined as
It is often abbreviated as CDF, and it has the following properties.
\(\lim_{x\to-\infty}F\left(x\right)=0\),
\(\lim_{x\to\infty}F\left(x\right)=1\),
non-decreasing,
right-continuous \(\lim_{y\to x^{+}}F\left(y\right)=F\left(x\right).\)
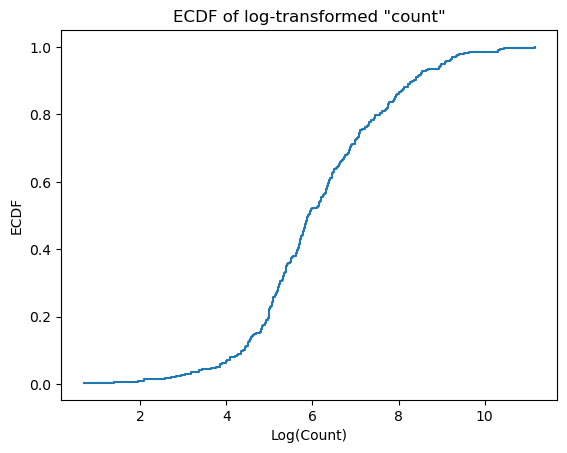
# Assuming d1_log is a DataFrame and 'count' is a column in d1_log
# Calculate the ECDF for the 'count' column
x = np.sort(d1_log['count'])
y = np.arange(1, len(x)+1) / len(x)
# Plot the ECDF as a step plot
plt.step(x, y, where='post')
plt.xlabel('Log(Count)')
plt.ylabel('ECDF')
plt.title('ECDF of log-transformed "count"')
plt.show()
The \(q\)-th quantile of a random variable is \(\min_{x\in \mathbb R} P(X \leq x) \geq q\).
d1_log['count'].quantile([0.25, 0.5, 0.75, 1.0])
0.25 5.087596
0.50 5.899897
0.75 7.107425
1.00 11.164587
Name: count, dtype: float64
For a continuous distribution, if its CDF is differentiable, then
is called the probability density function of \(X\), often abbreviated as PDF. It is easy to show that \(f\left(x\right)\geq0\), and by the Leibniz integral rule \(\int_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)\).
For a discrete random variable, its CDF is obviously non-differentiable at any jump points. In this case, we define the probability mass function \(f(x) = F(x) - \lim_{y \to x^{-}} F(y)\).
We have learned many parametric distributions. A parametric distribution can be completely characterized by a few parameters.
Examples
Binomial distribution.
Poisson distribution.
Uniform distribution.
Normal distribution.
Its mean is \(\mu\) and variance \(\sigma^2\).
Log-normal distribution.
Its means is \(\exp(\mu + 0.5 \sigma^2)\) and variance \([\exp(\sigma^2 - 1)] \exp(2\mu+ \sigma^2)\).
\(\chi^{2}\), \(t\), and \(F\) distributions.
Example
scipy.stat has a rich collection of distributions.
from scipy.stats import norm
# Calculate the 97.5th percentile of the standard normal distribution
norm.ppf(0.975)
np.float64(1.959963984540054)
norm.cdf(0)
np.float64(0.5)
norm.pdf(0)
np.float64(0.3989422804014327)
np.random.normal(loc=0, scale=1, size=3)
array([-0.04551741, 0.90159374, 0.21419417])
np.random.poisson(lam=5, size=3)
array([6, 4, 4])
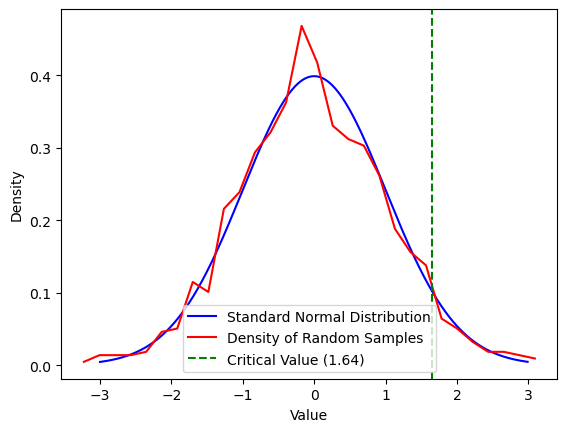
Below is a piece of code for demonstration.
Plot the density of standard normal distribution over an equally spaced grid system.
Generate 1000 observations for \(N(0,1)\). Plot the histogram density, a nonparametric estimation of the density.
Calculate the 95th quantile and the empirical probability of observing a value greater than the 95th quantile. In population, this value is 5%. What is the number coming out of this experiment?
(Since we do not fix the random seed in the computer, the outcome is slightly different each time when we run the code.)
# Create x-axis from -3 to 3 with steps of 0.01
x_axis = np.arange(-3, 3, 0.01)
# Calculate the density of the standard normal distribution for x_axis
y = norm.pdf(x_axis)
# Plot the standard normal distribution density
plt.plot(x_axis, y, label='Standard Normal Distribution', color='blue')
plt.xlabel('Value')
plt.ylabel('Density')
# Generate 1000 random samples from a standard normal distribution
z = np.random.normal(size=1000)
# Calculate the density of the random samples and plot it
density = np.histogram(z, bins=30, density=True)
bin_centers = 0.5*(density[1][1:] + density[1][:-1])
plt.plot(bin_centers, density[0], color='red', label='Density of Random Samples')
# Calculate the critical value at the 95th percentile
crit = norm.ppf(0.95)
# Calculate the empirical rejection probability
empirical_rejection_probability = np.mean(z > crit)
print(f"The empirical rejection probability is {empirical_rejection_probability}")
# Add a vertical line for the critical value
plt.axvline(crit, color='green', linestyle='--', label=f'Critical Value ({crit:.2f})')
plt.legend()
plt.show()
The empirical rejection probability is 0.051
Integration#
In probability theory, an integral \(\int X\mathrm{d}P\) is called the expected value, or expectation, of \(X\). We often use the notation \(E\left[X\right]\), instead of \(\int X\mathrm{d}P\), for convenience.
The expectation is the average of a random variable, despite that we cannot foresee the realization of a random variable in a particular trial (otherwise there is no uncertainty). In the frequentist’s view, the expectation is the average outcome if we carry out a large number of independent trials.
If we know the probability mass function of a discrete random variable, its expectation is calculated as \(E\left[X\right]=\sum_{x}xP\left(X=x\right)\). If a continuous random variable has a PDF \(f(x)\), its expectation can be computed as \(E\left[X\right]=\int xf\left(x\right)\mathrm{d}x\).
np.mean( d1_log["count"] )
np.float64(6.146389135729357)
Here are some properties of the expectation.
\(E\left[X^{r}\right]\) is call the \(r\)-moment of \(X\). The mean of a random variable is the first moment \(\mu=E\left[X\right]\), and the second centered moment is called the variance \(\mathrm{var}\left[X\right]=E [(X-\mu)^{2}]\).
np.var(d1_log["count"])
np.float64(2.6415986858999068)
The third centered moment \(E\left[\left(X-\mu\right)^{3}\right]\), called skewness, is a measurement of the symmetry of a random variable, and the fourth centered moment \(E\left[\left(X-\mu\right)^{4}\right]\), called kurtosis, is a measurement of the tail thickness.
We call \(E\left[\left(X-\mu\right)^{3}\right]/\sigma^{3}\) the skewness coefficient, and \(E\left[\left(X-\mu\right)^{4}\right]/\sigma^{4}-3\) degree of excess. A normal distribution’s skewness and degree of excess are both zero.
Moments do not always exist. For example, the mean of the Cauchy distribution does not exist, and the variance of the \(t(2)\) distribution does not exist.
\(E[\cdot]\) is a linear operation. \(E[a X_1 + b X_2] = a E[X_1] + b E[X_2].\)
Jensen’s inequality is an important fact. A function \(\varphi(\cdot)\) is convex if \(\varphi( a x_1 + (1-a) x_2 ) \leq a \varphi(x_1) + (1-a) \varphi(x_2)\) for all \(x_1,x_2\) in the domain and \(a\in[0,1]\). For instance, \(x^2\) is a convex function. Jensen’s inequality says that if \(\varphi\left(\cdot\right)\) is a convex function, then
\[ \varphi\left(E\left[X\right]\right)\leq E\left[\varphi\left(X\right)\right]. \]Markov inequality is another simple but important fact. If \(E\left[\left|X\right|^{r}\right]\) exists, then
\[ P\left(\left|X\right|>\epsilon\right)\leq E\left[\left|X\right|^{r}\right]/\epsilon^{r} \]for all \(r\geq1\). Chebyshev inequality \(P\left(\left|X\right|>\epsilon\right)\leq E\left[X^{2}\right]/\epsilon^{2}\) is a special case of the Markov inequality when \(r=2\).
Multivariate Random Variable#
A bivariate random variable is a vector of two scalar random variables. More generally, a multivariate random variable has the joint CDF as
Joint PDF is defined similarly.
# Plotting 'subs' on the x-axis and 'view' on the y-axis
plt.plot(d1_log['subs'], d1_log['view'], marker='o', linestyle='None')
plt.xlabel('Subscribers')
plt.ylabel('Views')
plt.title('scatter plot')
plt.show()
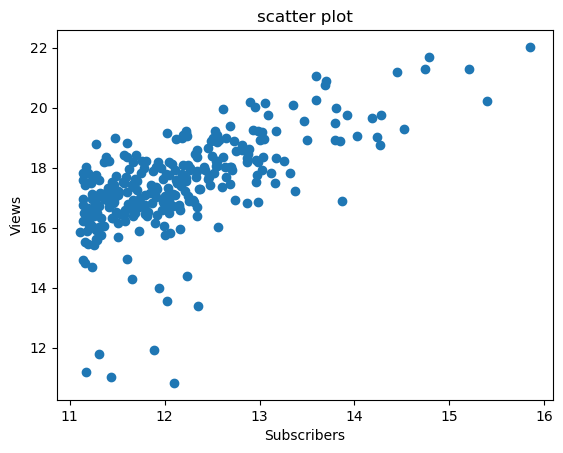
It is illustrative to introduce the joint distribution, conditional distribution and marginal distribution in the simple bivariate case, and these definitions can be extended to multivariate distributions. Suppose a bivariate random variable \((X,Y)\) has a joint density \(f(\cdot,\cdot)\). The marginal density \(f\left(y\right)=\int f\left(x,y\right)dx\) integrates out the coordinate that is not interested. The conditional density can be written as \(f\left(y|x\right)=f\left(x,y\right)/f\left(x\right)\) for \(f(x) \neq 0\).
Independence#
For two events \(A_1\) and \(A_2\), the conditional probability is
if \(P(A_2) \neq 0\). In this definition of conditional probability, \(A_2\) plays the role of the outcome space so that \(P(A_1 A_2)\) is standardized by the total mass \(P(A_2)\).
Since \(A_1\) and \(A_2\) are symmetric, we have \(P(A_1 A_2) = P(A_2|A_1)P(A_1)\). It implies
This formula is the well-known Bayes’ Theorem, which is a cornerstone of decision theory.
Example
\(A_1\) is the event “a student can survive CUHK’s MSc program”, and \(A_2\) is his or her application profile.
We say two events \(A_1\) and \(A_2\) are independent if \(P(A_1A_2) = P(A_1)P(A_2)\). If \(P(A_2) \neq 0\), it is equivalent to \(P(A_1 | A_2 ) = P(A_1)\). In words, knowing \(A_2\) does not change the probability of \(A_1\).
If \(X\) and \(Y\) are independent, then \(E[XY] = E[X]E[Y]\).
# Generate a 2-column matrix with 100 rows of random numbers from a standard normal distribution
Y = np.random.normal(size=(100, 2))
# Plot the first column against the second column
plt.scatter(Y[:, 0], Y[:, 1])
plt.xlabel('Column 1')
plt.ylabel('Column 2')
plt.title('Scatter plot of two normally distributed variables')
plt.show()
Y = np.random.normal(size=(100, 2))
# Apply the linear transformation
Y = np.dot(Y, np.array([[1, 0.5], [0.5, 1]]) )
# Plot the transformed data
plt.scatter(Y[:, 0], Y[:, 1])
plt.xlabel('Transformed Column 1')
plt.ylabel('Transformed Column 2')
plt.title('Scatter plot of transformed variables')
plt.show()
Law of Iterated Expectations#
In the bivariate case, if the conditional density exists, the conditional expectation can be computed as \(E\left[Y|X\right]=\int yf\left(y|X\right)dy\). The law of iterated expectation implies \(E\left[E\left[Y|X\right]\right]=E\left[Y\right]\).
# Add 'category' column from d0 to d1_log
d1_log['category'] = d0['category']
# Group by 'category' and calculate mean and count
dx = d1_log.groupby('category').agg(mean=('count', 'mean'), no=('count', 'size')).reset_index()
print(dx)
category mean no
0 Autos & Vehicles 7.516632 2
1 Comedy 5.742748 8
2 Education 6.290369 10
3 Entertainment 6.342173 41
4 Film & Animation 5.976671 28
5 Gaming 6.427200 28
6 Howto & Style 5.713592 31
7 Music 5.914223 24
8 News & Politics 8.134565 22
9 Nonprofits & Activism 6.445720 1
10 People & Blogs 5.724408 68
11 Pets & Animals 6.188264 1
12 Science & Technology 6.083646 8
13 Sports 6.140040 5
14 Travel & Events 5.483655 12
# Calculate weighted average over categories
weighted_avg = sum(dx['mean'] * (dx['no'] / len(d1_log)))
print(weighted_avg)
# Calculate and print overall average of 'count'
overall_avg = d1_log['count'].mean()
print(overall_avg)
6.146389135729356
6.146389135729357
Below are some properties of conditional expectations
\(E\left[E\left[Y|X_{1},X_{2}\right]|X_{1}\right]=E\left[Y|X_{1}\right];\)
\(E\left[E\left[Y|X_{1}\right]|X_{1},X_{2}\right]=E\left[Y|X_{1}\right];\)
\(E\left[h\left(X\right)Y|X\right]=h\left(X\right)E\left[Y|X\right].\)
Application
Regression is a technique that decomposes a random variable \(Y\) into two parts, a conditional mean and a residual. Write \(Y=E\left[Y|X\right]+\epsilon\), where \(\epsilon=Y-E\left[Y|X\right]\). Show that \(E[\epsilon] = 0\) and \(E[\epsilon E[Y|X] ] = 0\).
For the next lecture#
Save the following data files for the next lecture.
d1_log.to_csv('logYoutuber.csv', index=False)
# save a random subsmaple
d1_log_sub = d1_log.sample(n=100).to_csv('logYoutuber_sample.csv', index=False)